RSA算法中,为什么需要的是两个素数?
当前位置:点晴教程→知识管理交流
→『 技术文档交流 』
RSA算法是一种广泛使用的非对称加密技术,基于大数分解的困难性。本文将探讨为什么RSA算法需要两个素数,并以通俗易懂的例子解释其原理,同时提供专业分析和必要的数学背景。 在现代通信中,数据的安全性至关重要。RSA算法,由Ron Rivest、Adi Shamir和Leonard Adleman在1977年发明,提供了一种强大的加密手段。其安全性基于一个简单的事实:将两个大素数相乘相对容易,但反过来,将它们的乘积分解为原始素数却极其困难。 素数的重要性素数定义素数是指只能被1和它本身整除的大于1的自然数。例如,2、3、5、7等。 RSA算法中的素数RSA算法需要两个大素数,原因如下:
密钥生成过程密钥生成流程图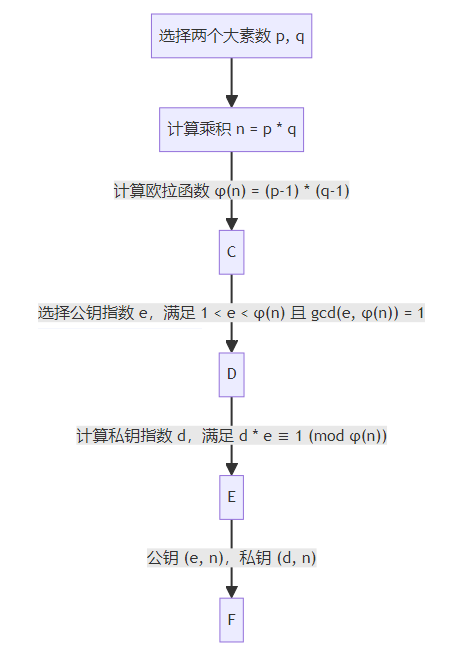 密钥生成详解
加密与解密过程加密过程假设Alice想要向Bob发送一条消息 ( M ),Bob的公钥是 ( (e, n) )。
解密过程Bob收到密文 ( c ) 后,使用他的私钥 ( (d, n) ) 解密。
安全性分析RSA算法的安全性依赖于大整数分解的难度。如果有人能够快速分解 ( n ),他们就可以计算出 ( φ(n) ),进而破解私钥 ( d )。然而,目前没有已知的算法能在合理时间内分解大整数。 RSA算法之所以需要两个素数,是因为它们提供了一种既简单又难以破解的方式来生成密钥。素数的选择和乘积的分解难度是RSA安全性的关键。随着计算技术的发展,RSA算法也在不断地进化,以保持其在数据安全领域的领先地位。 原文链接https://www.cnblogs.com/primihub/p/18241759 该文章在 2024/6/13 9:40:48 编辑过 |
关键字查询
相关文章
正在查询... |